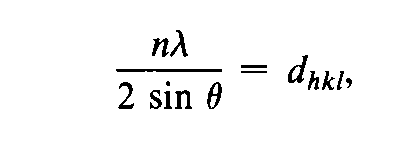Every crystal form of a compound produces its own characteristic X-ray diffraction pattern.These diffraction patterns can be derived either from a single crystal or from a powdered specimen (containing numerous crystals)of the material.The spacings between and the relative intensities of the diffracted maxima can be used for qualitative and quantitative analysis of crystalline materials.Powder diffraction techniques are most commonly employed for routine identification and the determination of relative purity of crystalline materials.Small amounts of impurity,however,are not normally detectable by the X-ray diffraction method,and for quantitative measurements it is necessary to prepare the sample carefully to avoid preferred orientation effects.

The powder methods provide an advantage over other means of analysis in that they are usually nondestructive in nature (specimen preparation is usually limited to grinding to ensure a randomly oriented sample,and deleterious effects of X-rays on solid pharmaceutical compounds are not commonly encountered).The principal use of single-crystal diffraction data is for the determination of molecular weights and analysis of crystal structures at the atomic level.However,diffraction established for a single crystal can be used to support a specific powder pattern as being truly representative of a single phase.

The relatively random arrangement of molecules in noncrystalline substances makes them poor coherent scatterers of X-rays,resulting in broad,diffuse maxima in diffraction patterns.Their X-ray patterns are quite distinguishable from crystalline specimens,which give sharply defined diffraction patterns.

Many compounds are capable of crystallizing in more than one type of crystal lattice.At any particular temperature and pressure,only one crystalline form (polymorph)is thermodynamically stable.Since the rate of phase transformation of a metastable polymorph to the stable one can be quite slow,it is not uncommon to find several polymorphs of crystalline pharmaceutical compounds existing under normal handling conditions.

In addition to exhibiting polymorphism,many compounds form crystalline solvates in which the solvent molecule is an integral part of the crystal structure.Just as every polymorph has its own characteristic X-ray patterns,so does every solvate.Sometimes the differences in the diffraction patterns of different polymorphs are relatively minor,and must be very carefully evaluated before a definitive conclusion is reached.In some instances,these polymorphs and/or solvates show varying dissolution rates.Therefore,on the time scale of pharmaceutical bioavailability,different total amounts of drug are dissolved,resulting in potential bioinequivalence of the several forms of the drug.

Afamily of planes in space can be indexed by three whole numbers,usually referred to as Miller indices.These indices are the reciprocals,reduced to smallest integers,of the intercepts that a plane makes along the axes corresponding to three nonparallel edges of the unit cell (basic crystallographic unit).The unit cell dimensions are given by the lengths of the spacings along the three axes,a,b,c,and the angles between them,a,b,and g.The interplanar spacing for a specific set of parallel planes hklis denoted by dhkl .Each such family of planes may show higher orders of diffraction where the dvalues for the related families of planes nh,nk,nlare diminished by the factor 1/n(nbeing an integer:2,3,4,etc.).Every set of planes throughout a crystal has a corresponding Braggs diffraction angle associated with it (for a specific l).

The amplitude of a diffracted X-ray beam from any set of planes is dependent upon the following atomic properties of the crystal:(1)position of each atom in the unit cell;(2)the respective atomic scattering factors;and (3)the individual thermal motions.Other factors that directly influence the intensities of the diffracted beam are:(1)the intensity and wavelength of the incident radiation;(2)the volume of crystalline specimen;(3)the absorption of the X-radiation by the specimen;and (4)the experimental arrangement utilized to record the intensity data.Thus,the experimental conditions are especially important for measurement of diffraction intensities.

Only a limited number of Braggs planes are in a position to diffract when monochromatized X-rays pass through a single crystal.Techniques of recording the intensities of all of the possible diffracting hklplanes involve motion of the single crystal and the recording media.Recording of these data is accomplished by photographic techniques (film)or with radiation detectors.

Abeam passing through a very large number of small,randomly oriented crystals produces continuous cones of diffracted rays from each set of lattice planes.Each cone corresponds to the diffraction from various planes having a similar interplanar spacing.The intensities of these Braggs reflections are recorded by either film or radiation detectors.The Braggs angle can be measured easily from a film,but the advent of radiation detectors has made possible the construction of diffractometers that read this angle directly.The intensities and dspacings are more conveniently determined with powder diffractometers employing radiation detectors than by film methods.Microphotometers are frequently used for precise intensity measurements of films.

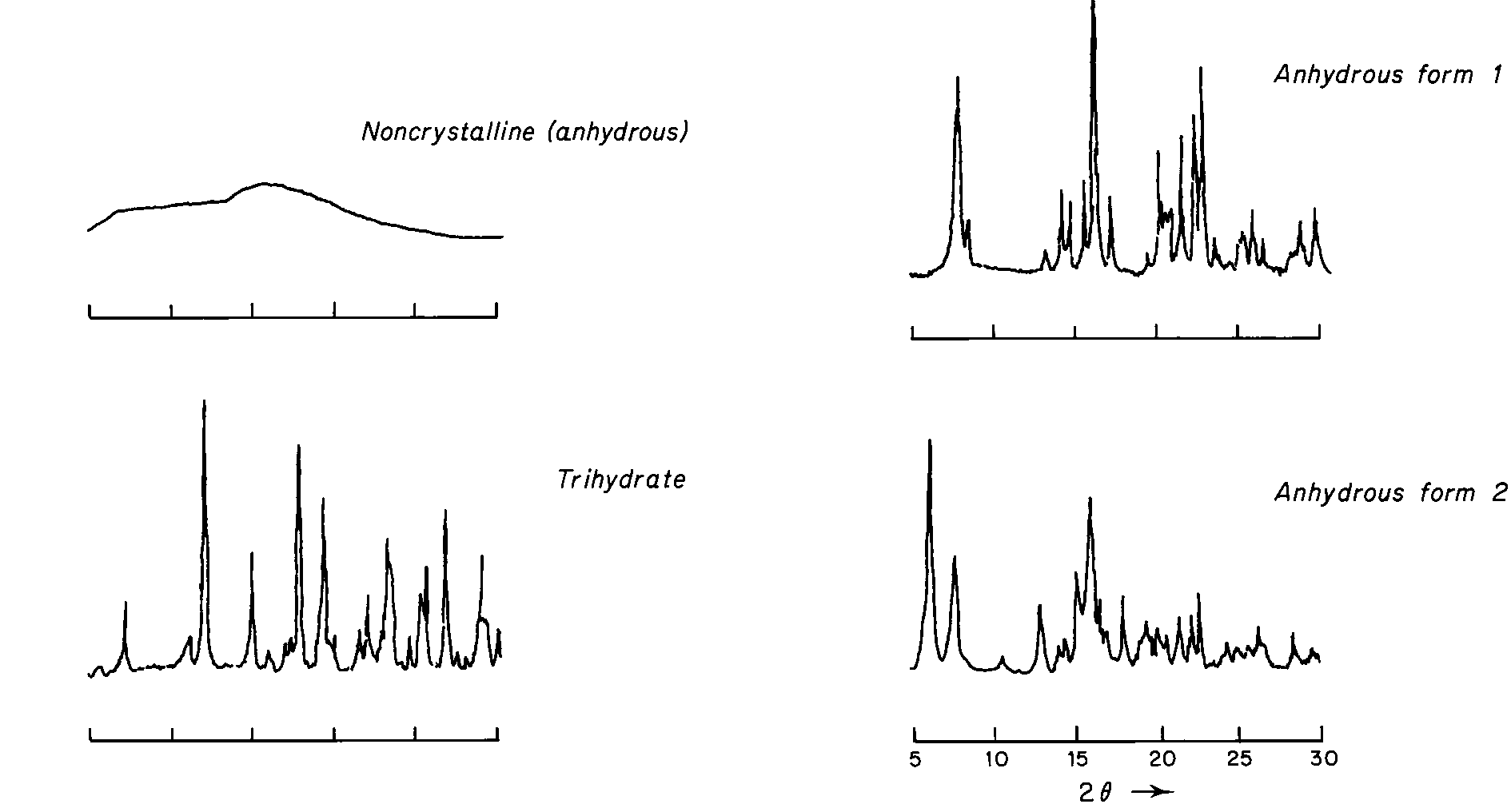
An example of the type of powder patterns obtained for four different solid phases of ampicillin are shown in the accompanying figure.

Typical Powder Patterns Obtained for Four Solid Phases of Ampicillin

These diffraction patterns were derived from a powder diffractometer equipped with a Geiger-Müller detector;nickel-filtered Cu Karadiation was used.

In general,the shapes of many crystalline particles tend to give a specimen that exhibits some degree of preferred orientation in the specimen holder.This is especially evident for needle-like or plate-like crystals where size reduction yields finer needles or platelets.Preferred orientation in the specimen influences the relative intensities of various reflections.

Several specialized handling techniques may be employed to minimize preferred orientation,but further reduction of particle size is often the best approach.

Where very accurate measurement of the Braggs angles is necessary,a small amount of an internal standard can be mixed into the specimen.This enables the film or recorder tracing to be calibrated.If comparisons to literature values (including compendial limits)of dare being made,calibrate the diffractometer.NISTstandards are available covering to a d-value of 0.998nm.Tetradecanol1may be used (dis 3.963nm)for larger spacing.

The absorption of the radiation by any specimen is determined by the number and kinds of atoms through which the X-ray beam passes.An organic matrix usually absorbs less of the diffracted radiation than does an inorganic matrix.Therefore,it is important in quantitative studies that standard curves relating amount of material to the intensity of certain dspacings for that substance be determined in a matrix similar to that in which the substance will be analyzed.

In quantitative analyses of materials,a known amount of standard usually is added to a weighed amount of specimen to be analyzed.This enables the amount of the substance to be determined relative to the amount of standard added.The standard used should have approximately the same density as the specimen and similar absorption characteristics.More important,its diffraction pattern should not overlap to any extent with that of the material to be analyzed.Under these conditions a linear relationship between line intensity and concentration exists.In favorable cases,amounts of crystalline materials as small as 10%may be determined in solid matrices.

Identification of crystalline materials can be accomplished by comparison of X-ray powder diffraction patterns obtained for known2materials with those of the unknown.The intensity ratio (ratio of the peak intensity of a particular dspacing to the intensity of the strongest maxima in the diffraction pattern)and the dspacing are used in the comparison.If a reference material (e.g.,USP Reference Standard)is available,it is preferable to generate a primary reference pattern on the same equipment used for running the unknown sample,and under the same conditions.For most organic crystals,it is appropriate to record the diffraction pattern to include values for 2qthat range from as near zero degrees as possible to 40degrees.Agreement between sample and reference should be within the calibrated precision of the diffractometer for diffraction angle (2qvalues should typically be reproducible to ±0.10degrees),while relative intensities between sample and reference may vary considerably.For other types of samples (e.g.,inorganic salts),it may be necessary to extend the 2qregion scanned to well beyond 40degrees.It is generally sufficient to scan past the ten strongest reflections identified in the Powder Diffraction File.2