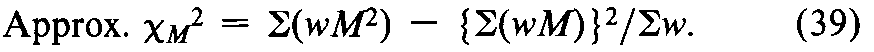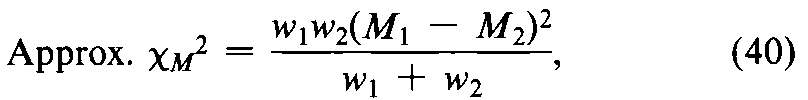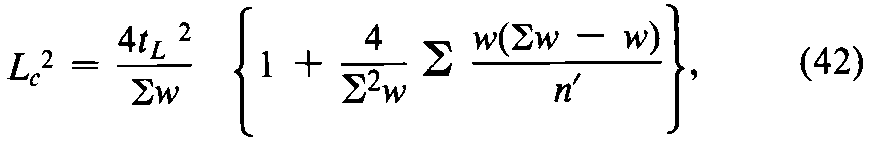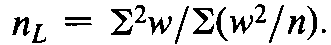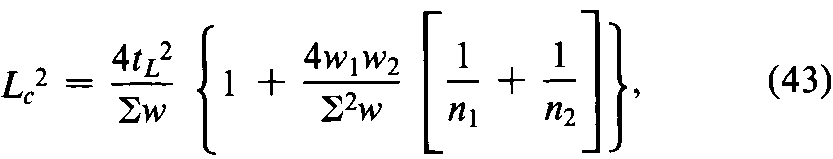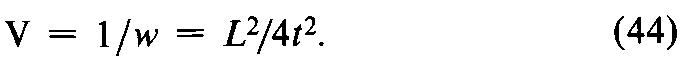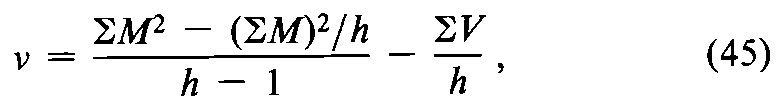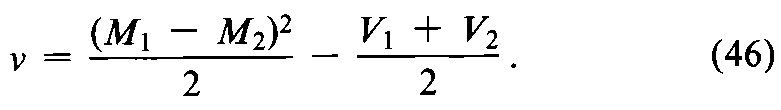When the method permits,additional animals can be added to an insufficiently precise assay until the combined results reduce the confidence interval within the limits specified in the monograph.Where two or more independent assays are required,each leading to a log-potencyM,theM's are combined in determining the weighted mean potencyof the Unknown.Except in the Heparin Sodium assay,where the log-potencies are weighted equally,the relative precisions of the two or more independentM's determine the weight assigned to each value in computing their mean and its confidence interval.

Before combining two or more separate estimates ofM,test their mutual consistency.If theM's are consistent,their respective confidence intervals will overlap.Where the intervals do not overlap or where the overlap is small,compute an approximate cM2.Assign each of the hindividual assays a weight w,defined as

where the length of the confidence interval Lis computed with the appropriate equation from the preceding section,and t2is read from Table 9for the degrees of freedom nin the error variance of the assay.Sum the individual weights to obtain Sw.Then an approximate c2with h–1degrees of freedom is determined as

For two assays with log-potenciesM1andM2and weights w1and w2,Equation 35reduces to

with one degree of freedom.If the approximate cM2is well under the critical value for c2in Table 9,use the weights win computing the mean log-potency bar(M)and its confidence interval,L.If cM2approaches or exceeds this critical value,use instead the semi-weights w¢(Equation 47)when computing bar(M).

Compute the mean log-potency bar(M)of two or more mutually consistent assays as

This is the most probable single value within a combined confidence interval of length Lc,defined as the square root of

where each n¢=n –4(h–2)/(h–1)and tL2is interpolated from Table 9with the degrees of freedom

For two assays (h=2)with log-potenciesM1andM2and weights w1and w2,respectively,the above equation may be rewritten as

where Sw =w1+w2.Where Lc,the confidence interval for a combined estimate,does not exceed the requirement in a monograph,upper and lower confidence limits are taken ½Lcabove and belowM,to obtain approximately a 95%confidence interval.

Where the variation in the assayed potency between the hindependent determinations,as tested by cM2,approaches or exceeds P=0.05,the several estimates are assigned semi-weights w¢.From the weight w,compute the variance of each Mas

Calculate the variance of the heterogeneity between assays as

or if h=2,

Where Vvaries so markedly that vcalculated as above is a negative number,compute instead an approximate vby omitting the term following the minus sign in Equations 45and 46.Asemi-weight is defined as

Substitute w¢and Sw¢for wand Swin Equation 41to obtain the semi-weighted mean bar(M).This falls near the middle of a confidence interval of approximate length Lc¢,where

and t2from Table 9has Sndegrees of freedom.

Where cM2in Equation 39,from h=4or more estimates ofM,exceeds the critical level in Table 9by more than 50%,and the weights wdiffer by less than 30%,the hestimates ofMmay be checked for a suspected outlier with Table 1.Where significant,the outlying Mmay be omitted in computing bar(M)with w¢.

Where the potency of a drug is determined repeatedly in a given laboratory by the same bioassay method,successive determinations of both the slope band the error variance s2may scatter randomly within the sampling error about a common value for each parameter.Plotting estimates from successive assays on a quality control chart for each statistic and computing the midvalue and control limits defining the allowable random variation make it possible to check continuously the consistency of an assay technique.Where estimates of band s2from a single assay fall within the control limits,they may be replaced by their laboratory means.Reject any assay in which these statistics fall outside the control limits,or accept it only after close scrutiny with respect to its validity.